A 2 − a 1 = 11−7 = 4 a 3 − a 2 = 15−11 = 4 a 4 − a 3 = 19−15 = 4 Hence, a k 1 − a k is the same value every time Therefore, this is an AP with
Find the sum of first 15 terms if an=3+4n-=(34n) of an a p then the sum of the its 15 terms is Medium Solution Verified by Toppr First terms t 1 =34=7 15th term =34×15=63 ∴S 15 = 215 t 1 t 15 215 (763)=15×35=525 Was this answer helpful? Where, a = the first term l = the last term Putting n = 1 in the given an, we get a = 3 4 (1) = 3 4 = 7 For the last term (l), here n = 15 a15 = 3 4 (15) = 63 So, Sn = 15(7 63) 2 15 ( 7 63) 2 = 15 x 35 = 525 Therefore, the sum of the 15 terms of the given AP is S15 = 525
Find the sum of first 15 terms if an=3+4nのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 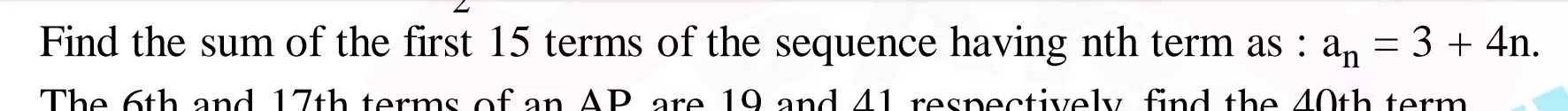 |
 | :max_bytes(150000):strip_icc()/dotdash_Final_Balance_Sheet_Aug_2020-01-4cad5e9866c247f2b165c4d9d4f7afb7.jpg) | |
 |  |  |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
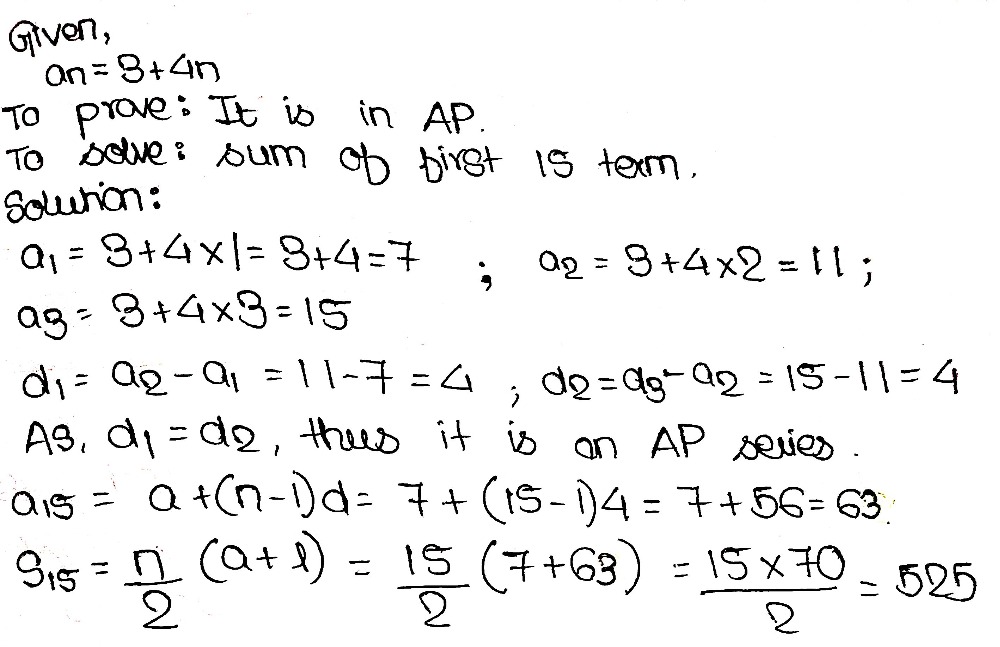 |  |  |
 |  | |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 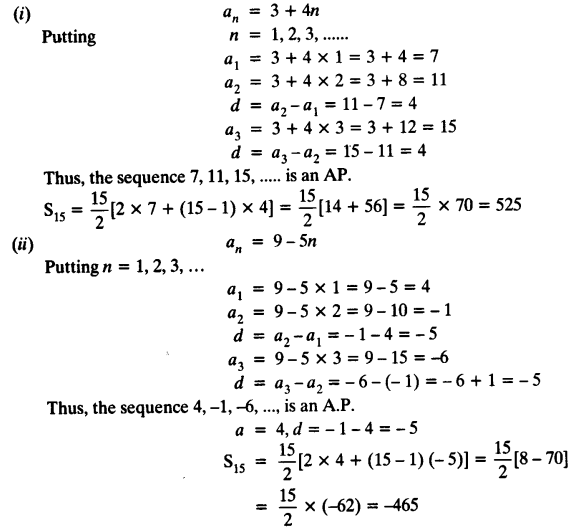 |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
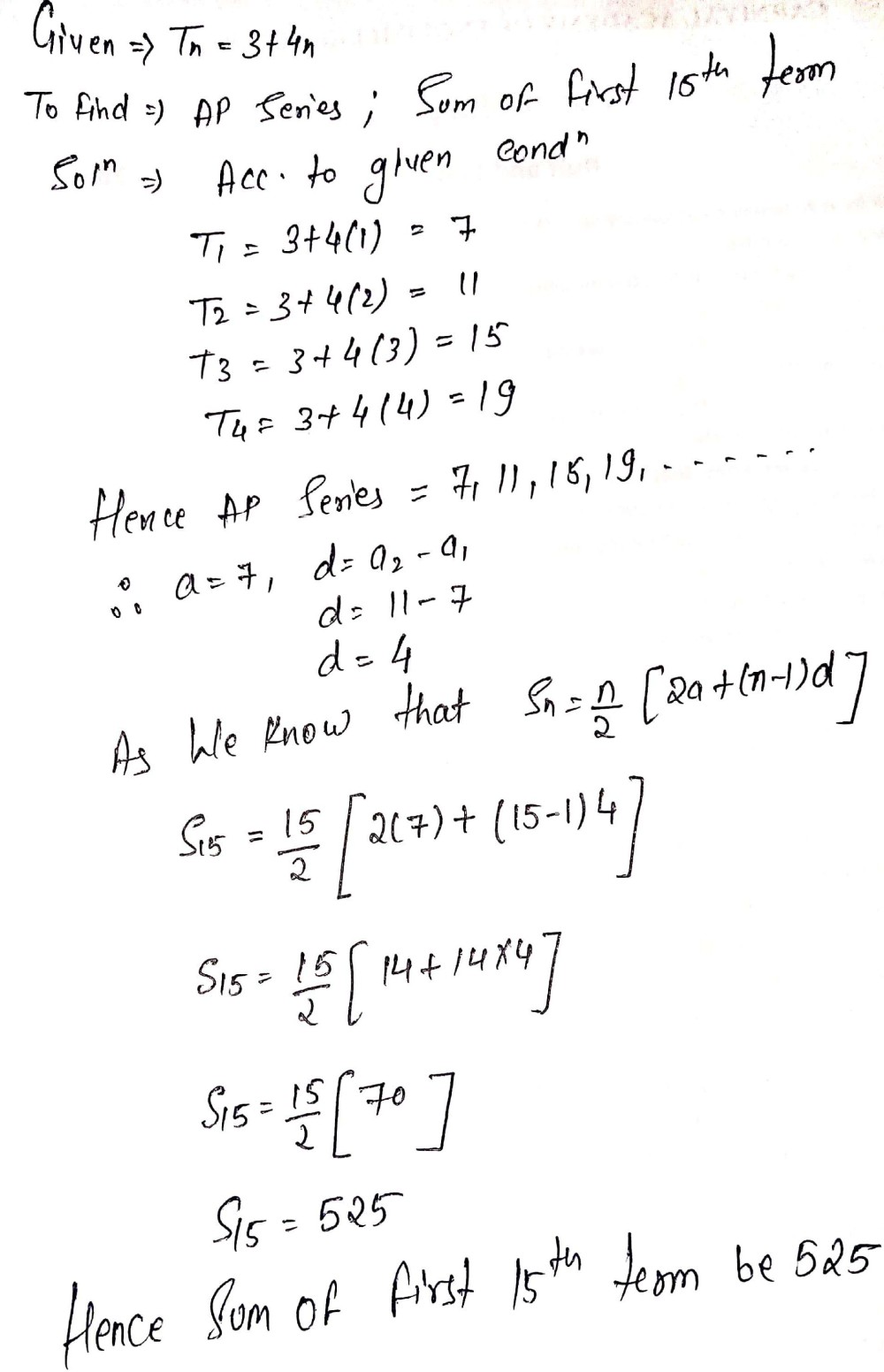 |  | |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | _1468216008_578332c87f791_217414-32.jpg) |  |
 |  |  |
 | ||
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Find the sum of first 15 terms if an=3+4n」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
tn = 3 4n To find The AP and sum of its first 15 terms Solution As given, The nth term is given by tn = 3 4n On putting n = 1 t1 = 7 Similarly, on putting n = 2 t2 = 3 4(2) = 11 when n = 3 t3 = 3 4(3) = 15 Hence, the AP is 7, 11, 15 Now, first term or a = 7 the common difference = 2nd term 1st term = 117 = 4 So, The sum of n terms− a3 = 19 − 15 = 4 ie, ak 1 − ak is same every time Therefore, this is an AP with common difference as 4 and first term as 7 S n = n 2 2 a ( n 1) d S 15 = 15 2 2 ( 7) ( 15 1) × 4 = 15/2 (14) 56 = 15/2 (70) = 15 × 35 = 525
Incoming Term: find the sum of first 15 terms if an=3+4n,




0 件のコメント:
コメントを投稿